Przekształcamy równania do postaci kierunkowej i wykorzystujemy interpretację geometryczną układów równań:

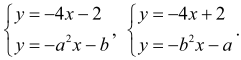
Układ jest sprzeczny, gdy proste o tych równaniach są równoległe, ale nie pokrywają się, stąd

(a² = 4 i b ≠ 2), czyli (a = 2 lub a = –2) i b ≠ 2.

Układ ma nieskończenie wiele rozwiązań, gdy proste o tych równaniach się pokrywają, tzn.

(b² = 4 i a = –2), więc (b = 2 lub b =–2) i a =–2.

Ostatecznie otrzymujemy, że

a = –2 i b = –2