Przyjmijmy oznaczenia:

x — długość dłuższego boku prostokąta,

x–5 — długość krótszego boku prostokąta.

Ponieważ długość boku ma wartość dodatnią, to

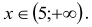
Pole prostokąta jest mniejsze od 24, zatem

Przekształcamy nierówność tak, aby po jednej stronie występowała liczba 0:

Rozwiązujemy nierówność w zbiorze

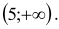
Obliczamy miejsca zerowe funkcji kwadratowej

y = x²–5x–24: x₁=–3, x₂=8

i szkicujemy fragment jej wykresu.

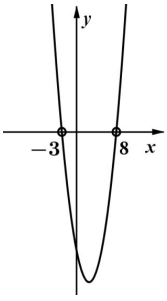
Odczytujemy  z  wykresu  rozwiązanie  nierówności  kwadratowej:

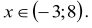
Uwzględniając warunki zadania, otrzymujemy warunek:

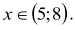
Z treści zadania wynika, że długość dłuższego boku prostokąta jest liczbą parzystą, zatem x = 6.

Odpowiedź: Długość dłuższego boku prostokąta jest równa 6.