Odpowiedź:
I sposób:
Wprowadzamy oznaczenia:
w — wydajność godzinowa II pompy (wyrażająca część objętości basenu),1,2w — wydajność godzinowa I pompy.
Zapisujemy zależności w postaci równania, z wykorzystaniem danych dotyczących czasu napełniania basenu przez każdą z pomp:
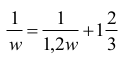
Przekształcamy do równania postaci:
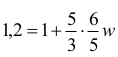
Wyznaczamy w = 0,1 [objętości basenu].
Zatem wydajność I pompy jest równa
1,2w = 1,2 · 0,1 = 0,12 [objętości basenu].
Obliczamy, jaką część pustego basenu napełnią w ciągu jednej godziny obie pompy, pracując jednocześnie:
0,12 + 0,1 = 0,22
Obie pompy, pracując jednocześnie, napełnią 0,22 objętości basenu.
II sposób
Wprowadzamy oznaczenia:
t — czas napełniania zbiornika tylko I pompą,
t — czas napełniania zbiornika tylko I pompą,
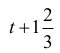 — czas napełniania zbiornika tylko II pompą.
— czas napełniania zbiornika tylko II pompą.Zapisujemy zależności w postaci równania, z wykorzystaniem danych dotyczących wydajności napełniania basenu przez każdą z pomp:
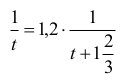
zatem
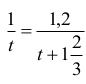
Przekształcamy do równania postaci:
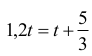
Wyznaczamy
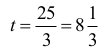 godziny.
godziny.Otrzymujemy
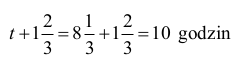
Czas napełniania basenu tylko I pompą jest równy 25/3 godziny, zatem w ciągu jednej godziny pompa ta napełni 3/25 objętości basenu.
Czas napełniania basenu tylko II pompą jest równy 10 godzin, zatem w ciągu jednej godziny pompa ta napełni 1/10 objętości basenu.
Obliczamy, jaką część pustego basenu napełnią w ciągu jednej godziny obie pompy, pracując jednocześnie:
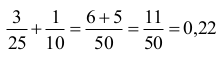
Obie pompy, pracując jednocześnie, napełnią 0,22 objętości basenu.