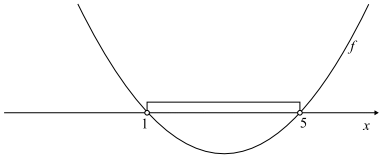
Z faktu, że rozwiązaniem nierówności ƒ(x)<0 są liczby rzeczywiste z przedziału (1,5), wynika, że parabola ma ramiona skierowane do góry, a miejscami zerowymi funkcji są liczby 1 i 5.




Wykres funkcji kwadratowej ƒ przesuwamy o trzy jednostki w lewo wzdłuż osi Ox. Miejscami zerowymi funkcji ƒ(x+3) są x = –2 i x = 2. Przekształcamy wykres funkcji ƒ(x+3)  symetrycznie względem osi Ox. To przekształcenie zmienia kierunek ramion paraboli, ale nie zmienia punktów leżących na osi Ox, więc liczby x = –2 i x = 2 są miejscami zerowymi funkcji –ƒ(x+3) .