Miejscami zerowymi funkcji ƒ są liczby –2 i 4, zatem pierwsza współrzędna wierzchołka paraboli, która jest wykresem funkcji ƒ, jest równa średniej arytmetycznej miejsc zerowych:

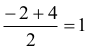
Z treści zadania wynika, że ƒ(1) = 3, zatem druga współrzędna wierzchołka paraboli jest równa 3. Funkcja kwadratowa ƒ ma dwa miejsca zerowe oraz wierzchołek paraboli leży powyżej osi Ox, zatem parabola ma ramiona skierowane do dołu. Prosta y = 2 jest równoległa do osi Ox i leży poniżej wierzchołka paraboli skierowanej ramionami do dołu, zatem przecina wykres funkcji ƒ w dwóch punktach symetrycznych względem prostej x = 1. Co kończy uzasadnienie.

Uwaga: Sytuację można przedstawić graficznie.

Miejscami zerowymi funkcji ƒ są liczby –2 i 4 , zatem

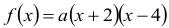
Obliczamy współczynnik a, korzystając z informacji, że

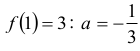
Z tego wynika, że

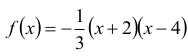
Wykres funkcji ƒ ma dwa punkty wspólne z prostą y = 2, gdy równanie

ma dwa rozwiązania.

Równanie to przekształcamy równoważnie:

x² – 2x – 2 = 0

Równanie kwadratowe ma dwa rozwiązania, jeżeli wyróżnik trójmianu kwadratowego jest większy od zera. Obliczamy wyróżnik równania

x² – 2x – 2 = 0: Δ = 4 – 4 · (–2) =12 > 0

Ponieważ

zatem wzór funkcji kwadratowej ƒ(x) =ax² + bx + c można wyznaczyć, rozwiązując układ równań