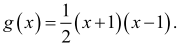Odpowiedź:
Obliczmy wyróżnik i miejsca zerowe funkcji ƒ określonej wzorem
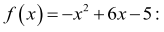
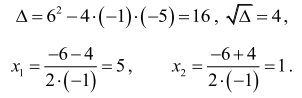
Ponieważ mniejsze z miejsc zerowych funkcji ƒ to także miejsce zerowe funkcji g, więc tym
miejscem zerowym jest liczba 1.
Wierzchołek paraboli, która jest wykresem funkcji ƒ, to punkt W o współrzędnych

Ponieważ wierzchołek Z paraboli, która jest wykresem funkcji g, leży na osi Oy układu współrzędnych, to oś Oy układu współrzędnych jest osią symetrii tej paraboli. Wzór funkcji g ma
więc postać
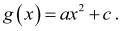
Punkt W = (3,4) leży na wykresie funkcji g, więc g(3) = 4, czyli
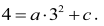
Liczba 1 jest miejscem zerowym funkcji g, więc g(1) = 0 , czyli
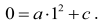
Stąd c = –a.
Zatem równanie
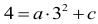
możemy zapisać w postaci
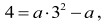
skąd otrzymujemy a = ½, a dalej c = –a = – ½
Wzór funkcji g ma zatem postać
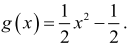
Uwaga
Wiedząc, że jednym z miejsc zerowych funkcji g jest liczba 1 i że oś Oy układu współrzędnych jest osią symetrii tej paraboli, możemy zapisać wzór funkcji g w postaci
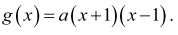
Punkt W = (3,4) leży na wykresie funkcji g, więc g(3) = 4, czyli
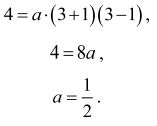
Wzór funkcji g ma zatem postać