Odpowiedź:
Zbadajmy zbiór wartości funkcji
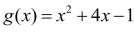
Zauważmy, że funkcja g jest rosnąca w przedziale ⟨–2,+∞).
Zatem funkcja g ma wartość najmniejszą w punkcie x = 1 i jest ona równa g(1) = 4. Wobec faktu, że funkcja g w przedziale ⟨1,3⟩ jest rosnąca i przyjmuje tylko wartości dodatnie, funkcja ƒ przyjmuje wartość największą w takim punkcie, w jakim funkcja g przyjmuje wartość najmniejszą.
Odpowiedź: Największa wartość funkcji jest równa 1/4
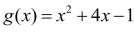
w przedziale ⟨1,3⟩.
Funkcja g przyjmuje wartość najmniejszą w punkcie x = –2, lecz –2∉⟨1,3⟩.
Zatem funkcja g ma wartość najmniejszą w punkcie x = 1 i jest ona równa g(1) = 4. Wobec faktu, że funkcja g w przedziale ⟨1,3⟩ jest rosnąca i przyjmuje tylko wartości dodatnie, funkcja ƒ przyjmuje wartość największą w takim punkcie, w jakim funkcja g przyjmuje wartość najmniejszą.
Odpowiedź: Największa wartość funkcji jest równa 1/4