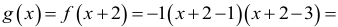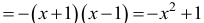Odpowiedź:
I sposób
Osią symetrii paraboli jest prosta x = 2. Wierzchołek paraboli ma współrzędne (2,q). Przesuwamy parabolę o 2 jednostki w lewo (wzdłuż osi Ox), tak żeby wierzchołek paraboli leżał
na osi Oy.
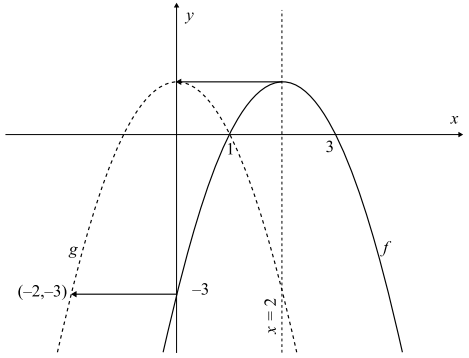
Miejscami zerowymi funkcji g są x = –1 oraz x = 1.
Zapisujemy wzór funkcji g w postaci iloczynowej
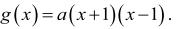
Punkt (–2,–3) należy do wykresu funkcji g, więc otrzymujemy
–3 = a(–2+1)(–2–1), stąd a = –1.
Ostatecznie otrzymujemy
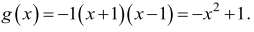
II sposób
Miejscami zerowymi funkcji ƒ są liczby 1 oraz 3, więc zapisujemy wzór funkcji ƒ w postaci
iloczynowej:
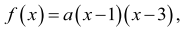
a następnie wykorzystujemy informację, że ƒ(0) = –3,
czyli
–3 = a(0–1)(0–3), stąd a = –1.
Otrzymaliśmy wzór funkcji
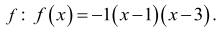
Osią symetrii paraboli, która jest wykresem funkcji ƒ, jest prosta x = 2 i na niej leży wierzchołek paraboli. Wierzchołek paraboli, która jest wykresem funkcji g, leży na osi Oy, stąd
wnioskujemy, że wykonano przesunięcie wykresu funkcji ƒ o dwie jednostki w lewo
(wzdłuż osi Ox).
Stąd otrzymujemy g(x) = ƒ(x+2).
Wyznaczamy wzór funkcji g: