Odpowiedź:
I sposób
Jeżeli wierzchołek paraboli, która jest wykresem funkcji ƒ, leży na prostej y = –5, to druga
współrzędna wierzchołka jest równa: q = –5.
Korzystając ze wzoru na drugą współrzędną wierzchołka paraboli, otrzymujemy:
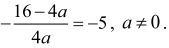
Przekształcając tę równość w sposób równoważny, otrzymujemy
a = 2/3.
Pierwsza współrzędna wierzchołka paraboli, która jest wykresem funkcji ƒ opisanej wzorem
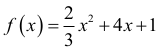
jest równa:
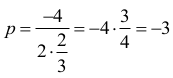
II sposób
Jeżeli wierzchołek paraboli, która jest wykresem funkcji ƒ, leży na prostej o równaniu y = –5 , to druga współrzędna wierzchołka jest równa: q = –5.
Korzystając ze wzoru na pierwszą współrzędną wierzchołka paraboli, otrzymujemy:
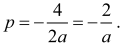
Korzystając z zależności ƒ(p) = q, otrzymujemy równość:
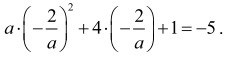
Przekształcając tę równość w sposób równoważny, otrzymujemy
a = 2/3
Pierwsza współrzędna wierzchołka paraboli, która jest wykresem funkcji ƒ, jest równa
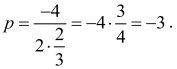
Zatem wierzchołek paraboli, która jest wykresem funkcji ƒ, ma współrzędne (–3,–5).