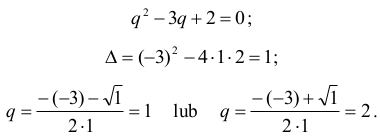Odpowiedź:
Oznaczamy: q — iloraz ciągu (an).
Z warunków zadania wynika, że
a5 – a3 = 3(a4 – a3)
oraz wyrazy ciągu (an) są różne od 0,
ponadto q jest różne od 0 i od 1, ponieważ wszystkie wyrazy ciągu są różne.
Ponieważ a5 = a3q2 oraz a4 = a3q , otrzymujemy równanie:
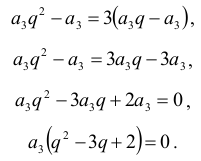
Ponieważ a3 ≠ 0, to