Odpowiedź:
I sposób
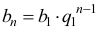
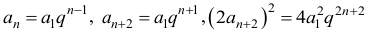
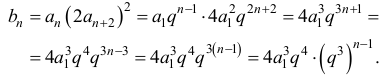
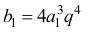
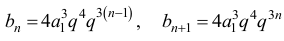
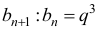
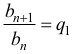
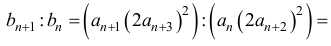
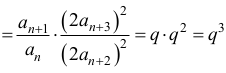
Aby wykazać, że ciąg (bn) jest ciągiem geometrycznym, wykażemy, że istnieje liczba q1 taka, że dla każdego n ≥ 1 prawdziwa jest równość
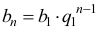
Oznaczmy przez q iloraz ciągu geometrycznego (an). Wtedy
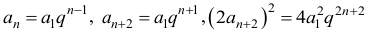
Stąd
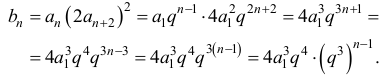
Ciąg (bn) jest więc ciągiem geometrycznym o pierwszym wyrazie
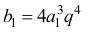
oraz ilorazie q1 równym q3 .
Uwaga: Można też zapisać, że
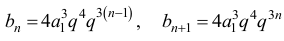
i sprawdzić, że dla każdego n ≥ 1 prawdziwa jest równość
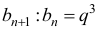
II sposób
Aby wykazać, że ciąg (bn) jest ciągiem geometrycznym, wykażemy, że istnieje liczba q1 taka, że dla każdego n ≥ 1 prawdziwa jest równość
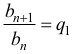
Oznaczmy przez q iloraz ciągu (an). Dla n ≥ 1 mamy
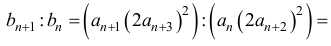
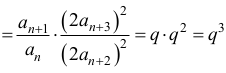
czyli ciąg (bn) jest geometryczny o ilorazie q1=q3.
Ciąg (bn) jest więc ciągiem geometrycznym o ilorazie równym q3 .