Odpowiedź:
Liczb całkowitych dodatnich parzystych nie większych od 1000 jest 500. Obliczamy sumę
wszystkich liczb naturalnych parzystych nie większych od 1000, korzystając ze wzoru na sumę n początkowych wyrazów ciągu arytmetycznego:
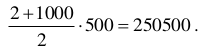
Liczby całkowite dodatnie parzyste podzielne przez 3 zapisujemy w postaci: 6x , gdzie x jest liczbą całkowitą dodatnią. Największą liczbą parzystą podzielną przez 3 i nie większą od 1000 jest 996, zatem liczb całkowitych dodatnich podzielnych przez 6 jest 166 (liczb od 1 do 996 jest 996, z czego co szósta będzie podzielna przez 6, stąd 996 : 6 = 166).
Obliczamy sumę wszystkich liczb naturalnych parzystych podzielnych przez 6, korzystając ze wzoru na sumę n początkowych wyrazów ciągu arytmetycznego:
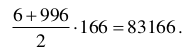
Obliczamy sumę wszystkich parzystych liczb całkowitych dodatnich nie większych od 1000 i niepodzielnych przez 3:
250500 – 83166 = 167334
Odpowiedź: Suma wszystkich parzystych liczb całkowitych dodatnich nie większych od 1000 i niepodzielnych przez 3 jest równa 167334.
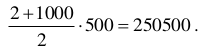
Liczby całkowite dodatnie parzyste podzielne przez 3 zapisujemy w postaci: 6x , gdzie x jest liczbą całkowitą dodatnią. Największą liczbą parzystą podzielną przez 3 i nie większą od 1000 jest 996, zatem liczb całkowitych dodatnich podzielnych przez 6 jest 166 (liczb od 1 do 996 jest 996, z czego co szósta będzie podzielna przez 6, stąd 996 : 6 = 166).
Obliczamy sumę wszystkich liczb naturalnych parzystych podzielnych przez 6, korzystając ze wzoru na sumę n początkowych wyrazów ciągu arytmetycznego:
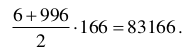
Obliczamy sumę wszystkich parzystych liczb całkowitych dodatnich nie większych od 1000 i niepodzielnych przez 3:
250500 – 83166 = 167334
Odpowiedź: Suma wszystkich parzystych liczb całkowitych dodatnich nie większych od 1000 i niepodzielnych przez 3 jest równa 167334.