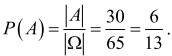Liczba wszystkich zdarzeń elementarnych doświadczenia losowego, w którym losujemy jedną przekątną spośród wszystkich przekątnych trzynastokąta, jest równa

|Ω|=65.

Niech A oznacza zdarzenie losowe polegające na wylosowaniu takiej przekątnej trzynastokąta, która przecina przekątną A₁A₈ w punkcie leżącym wewnątrz trzynastokąta. Zauważmy, że końce takiej przekątnej muszą leżeć po przeciwnych stronach prostej A₁A₈ . Ponieważ po jednej stronie tej prostej mamy 5, a po drugiej 6 wierzchołków trzynastokąta, to liczba tych przekątnych jest równa 5·6. Wobec tego liczba wszystkich przekątnych trzynastokąta, które przecinają przekątną A₁A₈ w punkcie leżącym wewnątrz trzynastokąta, jest równa

5·6=30 czyli |A|=30.

Prawdopodobieństwo zdarzenia A jest więc równe