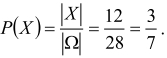Odpowiedź:
I sposób
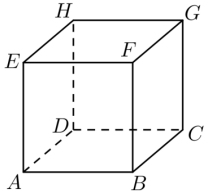
Oznaczamy przez A, B, C, D, E, F, G, H wierzchołki sześcianu (zobacz rysunek).
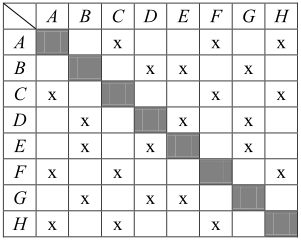
Wyniki losowania można przedstawić w tabeli. Pola położone na przekątnej odrzucamy, ponieważ nie możemy wylosować dwa razy tego samego wierzchołka.
Niech X oznacza zdarzenie polegające na wylosowaniu dwóch wierzchołków, które są końcami tej samej przekątnej ściany sześcianu (uwzględniamy kolejność wylosowanych wierzchołków). Zdarzenia elementarne sprzyjające zdarzeniu X zaznaczamy w tabeli krzyżykiem (x).
Z tego wynika, że mamy 56 wszystkich zdarzeń elementarnych, czyli
|Ω|=8·7=56,
oraz 24 zdarzenia elementarne sprzyjające zdarzeniu X, czyli
|x| = 8·3=24.
Prawdopodobieństwo zdarzenia X jest równe
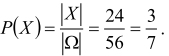
II sposób
Niech Ω oznacza zbiór wszystkich zdarzeń elementarnych doświadczenia polegającego
na losowaniu dwóch różnych wierzchołków sześcianu (bez uwzględniania kolejności wylosowania wierzchołków).
Obliczamy liczbę wszystkich zdarzeń elementarnych:
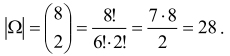
Niech X oznacza zdarzenie polegające na wylosowaniu dwóch wierzchołków, które są końcami tej samej przekątnej ściany sześcianu (nie uwzględniamy kolejności losowania wierzchołków). Każda z sześciu ścian sześcianu ma dwie przekątne, czyli
|X|=6·2=12.
Prawdopodobieństwo zdarzenia X jest równe
Prawdopodobieństwo zdarzenia X jest równe