Zauważmy, że równanie

k²x – 1 = x(3k – 2) – k

można zapisać w postaci

x(k² – 3k + 2)=1 – k

Po przekształceniu trójmianu

k² – 3k + 2

do postaci iloczynowej otrzymujemy

x(k – 1)(k – 2) = 1 – k

Zauważmy, że dla k≠1 oraz k≠2 otrzymujemy

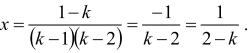
Dla k = 1 mamy: x(1 - 1)(1 - 2) = 1 - 1, czyli 0 = 0 — każda liczba jest rozwiązaniem, więc równanie ma nieskończenie wiele rozwiązań.

Dla k – 2 mamy: x(2-1)(2-2) = 1-2, czyli 0 = -1 — równanie nie ma rozwiązań.

Zatem dla każdej wartości parametru z wyłączeniem 2 równanie ma rozwiązanie.