Rozwiążemy nierówność w każdym z przedziałów wyznaczonych na osi liczbowej przez argumenty, dla których |2x – 2| = 0 oraz |x| = 0.

Ponieważ 2x – 2 = 0 dla x = 1, więc to liczby 0 i 1 wyznaczają podział.

Rozważymy naszą nierówność w każdym z przedziałów

(–∞,0), ⟨0,1) oraz ⟨1,+∞).

• Rozważmy nierówność

|2x – 2| ≥ x + |x| dla x∈(–∞,0).

Otrzymujemy wówczas, że

|x| = –x oraz |2x – 2| = –(2x – 2)

a nierówność przyjmuje postać

–(2x – 2) ≥ x + (–x)

Jej rozwiązaniem są liczby spełniające warunek:

x ≤ 1

Ponieważ rozważamy nierówność dla x∈(–∞,0), to otrzymujemy: x∈(–∞,0)

• Rozważmy teraz nierówność na przedziale ⟨0,1).

Otrzymujemy wówczas, że

|x| = x oraz |2x – 2| = –(2x – 2)

i nierówność przyjmuje postać

–(2x – 2) ≥ x + x

zatem x ≤ ½

Ponieważ rozważamy nierówność dla x∈⟨0,1), to otrzymujemy: x∈⟨0,½⟩

• Rozważmy teraz nierówność na przedziale ⟨1,+∞).

Otrzymujemy wówczas, że

|x| = x oraz |2x – 2| = (2x – 2)

x∈(–∞,0)∪⟨0,½⟩.

zatem

Zapiszmy nierówność w postaci

|2x – 2| ≥ x + |x|

Naszkicujmy wykresy funkcji

ƒ(x) = |2x – 2| oraz g(x) = x + |x|

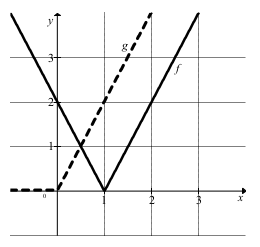
Z rysunku odczytujemy współrzędne punktu wspólnego obu wykresów:

(½,1) — możemy sprawdzić, że istotnie dla argumentu równego ½ wartości obu funkcji są równe 1. Zatem rozwiązaniem nierówności są wszystkie liczby ze zbioru (–∞,½⟩.