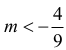Odpowiedź:
Dla m = 0 równanie przyjmuje postać: –1 = 0, czyli nie ma rozwiązań.
Dla m ≠ 0 równanie jest kwadratowe i możemy je zapisać w postaci:
m(x2 + x – 2) = 1
czyli
x2 + x – 2 = 1⁄m
Narysujmy wykres funkcji ƒ(x) = x2 + x – 2 dla x ∈ ⟨–2, 2⟩
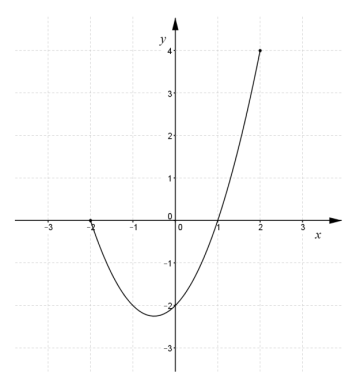
Zauważmy, że prosta o równaniu y = 1⁄m ma jeden punkt wspólny z wykresem funkcji wtedy i tylko wtedy, gdy
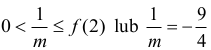
czyli
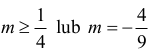
Prosta o równaniu y = 1⁄m ma dwa punkty wspólne z wykresem funkcji wtedy i tylko wtedy, gdy
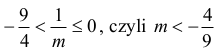
Prosta o równaniu y = 1⁄m nie ma punktów wspólnych z wykresem funkcji wtedy i tylko wtedy, gdy
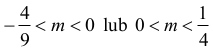
Odpowiedź:
Równanie mx2 + mx – 1 – 2m = 0, dla x ∈ ⟨–2, 2⟩
— nie ma rozwiązań wtedy i tylko wtedy, gdy
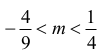
— ma jedno rozwiązanie wtedy i tylko wtedy, gdy
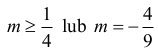
— ma dwa rozwiązania wtedy i tylko wtedy, gdy