Odpowiedź:
I sposób
Dla m = 1 wykresem funkcji ƒ jest prosta o równaniu y = –2x , która przecina się z prostą y = –x + 1 w jednym punkcie, więc dla m = 1 nie są spełnione warunki zadania.
Dla m ≠ 1 wykresem funkcji ƒ jest parabola, która ma z prostą o równaniu y = –x + 1 dwa punkty wspólne, gdy równanie
(m – 1)x2 – 2x – m + 1 = –x + 1
ma dwa rozwiązania.
Przekształcając je równoważnie, otrzymujemy równanie kwadratowe:
(m – 1)x2 – x – m = 0
Wyznaczamy wyróżnik:
Δ = 4m2 – 4m + 1 = (2m – 1)2
Rozważane równanie ma dwa rozwiązania x1, x2 , gdy Δ>0, czyli dla
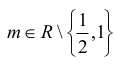
Rozwiązania x1, x2 , mają przeciwne znaki, gdy x1·x2<0
Korzystając ze wzoru Viète’a, możemy zapisać:
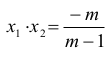
zatem
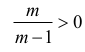
Nierówność jest prawdziwa dla
Z tego wynika, że wykres funkcji
przecina się z prostą
o równaniu y = –x + 1 w dwóch punktach, których pierwsze współrzędne mają przeciwne
znaki, gdy m ∈ (–∞,0)∪(1,+∞)
II sposób
Dla m = 1 wykresem funkcji ƒ jest prosta o równaniu y = –2x , która przecina się z prostą
o równaniu y = –x + 1 w jednym punkcie, czyli dla parametru m = 1 nie są spełnione warunki zadania.
Dla m ≠ 1 wyznaczamy pierwsze współrzędne punktów przecięcia się wykresu funkcji ƒ z prostą o równaniu y = –x + 1
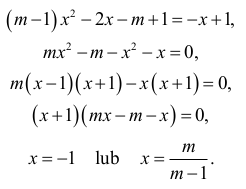
Ponieważ
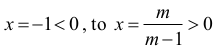
Z tego wynika, że
m(m – 1) > 0
czyli