Oznaczmy przez x₁, x₂ pierwiastki tego trójmianu.

Korzystając ze wzorów Viete’a, mamy:

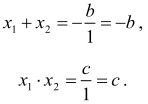
Sumę 1 + b + c możemy więc zapisać w postaci:

1 + b + c = 1 – x₁ – x₂ + x₁ · x₂ = (1 – x₁ )·(1 – x₂)

Zauważmy, że aby iloczyn p·q liczb całkowitych był liczbą pierwszą, to jedna z tych liczb musi być równa 1 lub –1.

Iloczyn (1–x₁)·(1–x₂) jest liczbą pierwszą i każda z liczb 1–x₁,1–x₂ jest całkowita, więc korzystając z powyższej uwagi, otrzymujemy, że jedna z nich musi być równa 1 lub –1.

Przypuśćmy, że 1 – x₁ = 1, wtedy mielibyśmy, że x₁ = 0, co jest sprzeczne z warunkami za­dania.

Przypuśćmy, że 1 – x₁ = –1, wtedy otrzymujemy, że x₁= 2

Trójmianem, który spełnia warunki zadania, jest na przykład:

x² – 6x + 8