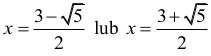Odpowiedź:
Równanie (x2 – 3x)(x2 – 3x + 2) + 1 = 0 możemy zapisać w postaci równoważnej:
(x2 – 3x)2 + (x2 – 3x) + 1 = 0
(x2 – 3x + 1)2 = 0
To równanie jest z kolei równoważne równaniu kwadratowemu x2 – 3x + 1 = 0, które ma dwa rozwiązania:
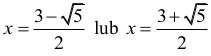
Uwaga:
Możemy też oznaczyć t = x2 – 3x i i wtedy równanie
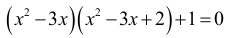
możemy zapisać w postaci
t(t + 2) + 1 = 0
Dalej mamy
t2 + 2t + 1= 0, (t + 1)2 = 0
Stąd t = -1
Wracając do przyjętego oznaczenia, otrzymujemy równanie kwadratowe
x2 – 3x = –1
To równanie jest równoważne równaniu kwadratowemu
x2 – 3x + 1 = 0
które ma dwa rozwiązania: