Odpowiedź:
Wyznaczamy pierwsze współrzędne punktów wspólnych wykresów funkcji ƒ i w:
x4 – 6x3 + 8x2 + 4x – 7 = –2x + 2
Przekształcamy równanie równoważnie:
x4 – 6x3 + 8x2 + 6x – 9 = 0
x4 – 6x3 + 9x2 – x2 + 6x – 9 = 0
x2(x2 – 6x + 9) – (x2 – 6x + 9) = 0
(x2 – 6x + 9)( x2 – 1) = 0
(x – 3)2 (x2 – 1) = 0
Powyższe
równanie jest spełnione, gdy
(x – 3)2 = 0
lub x2 – 1 = 0,
zatem
x = 3 lub x = -1, lub x = 1.
Z tego wynika, że istnieją dokładnie trzy punkty wspólne wykresów ƒ i w (zobacz rysunek).
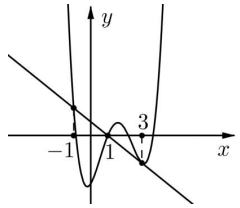
Z rysunku odczytujemy zbiór rozwiązań nierówności
w(x) ≥ ƒ(x): x ∈ (-∞; -1⟩ ∪ ⟨1; +∞).