Odpowiedź:
Rozwiązanie zadania składa się z dwóch etapów.
Pierwszy etap:
wyznaczenie współczynników liczbowych a i b funkcji kwadratowej ƒ.
Funkcja ƒ jest funkcją kwadratową, zatem a ≠ 0.
Ponieważ funkcja ƒ osiąga najmniejszą wartość dla argumentu 4, to
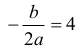
Ponadto ƒ(4) = –22 . Otrzymujemy zatem układ równań
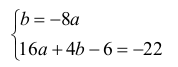
Powyższy układ równań spełnia tylko jedna para liczb: a = 1 i b = –8, zatem równanie ma postać
x3 + x2 – 8x – 6 = 0
Uwaga: Równanie b = –8a można otrzymać również, korzystając z własności pochodnej funkcji.
Współczynniki liczbowe a i b można wyznaczyć także, zapisując wzór funkcji kwadratowej ƒ w postaci kanonicznej:
ƒ(x) = a(x – 4)2 – 2
Następnie trzeba przekształcić ten wzór do postaci ogólnej i porównać odpowiednie współczynniki.
Drugi etap:
rozwiązanie równania
x3 + x2 – 8x – 6 = 0
Jednym z rozwiązań równania jest liczba -3 , zatem wielomian
W(x) = x3 + x2 – 8x – 6
jest podzielny przez dwumian x + 3
Dzielimy wielomiany:
(x3 + x2 – 8x – 6):(x + 3) = x2 –2x – 2
Pozostałe rozwiązania równania
x3 + x2 – 8x – 6 = 0
są pierwiastkami trójmianu kwadratowego x2 –2x – 2 :
x = 1 – √3 lub x = 1 + √3