Odpowiedź:
Stosując wzory skróconego mnożenia na sumę sześcianów i różnicę sześcianów, możemy
nierówność zapisać w postaci równoważnej
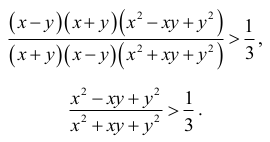
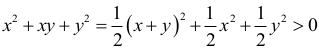
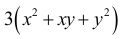
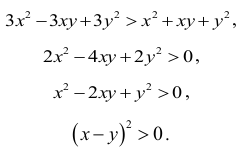
Ta nierówność jest prawdziwa, gdyż x ≠ y, a kwadrat liczby różnej od zera jest dodatni. To kończy dowód.
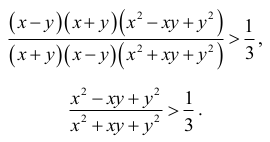
Ponieważ
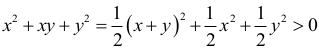
gdyż x ≠ – y , to mnożąc obie strony nierówności przez
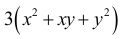
otrzymujemy nierówność równoważną
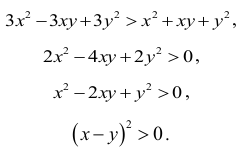
Ta nierówność jest prawdziwa, gdyż x ≠ y, a kwadrat liczby różnej od zera jest dodatni. To kończy dowód.