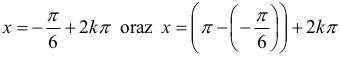Równanie możemy przekształcić w sposób równoważny:

Zauważmy, że ostatnie równanie jest równoważne alternatywie

2sin x + 1 = 0

lub

cos x + 1 = 0

Równanie 2sin x + 1 = 0 jest równoważne równaniu

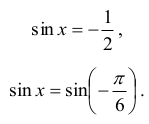
Zatem

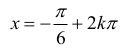
dla dowolnej liczby całkowitej k

lub

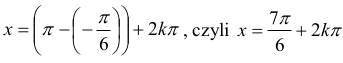
dla dowolnej liczby całkowitej k.

W zadanym przedziale rozwiązaniem są liczby

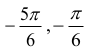
Równanie cos x + 1 = 0 jest równoważne równaniu

cos x = –1

cos x = cos(π)

zatem

x = π + 2kπ dla dowolnej liczby całkowitej k.

W zadanym przedziale rozwiązaniem są liczby – π, π.

Funkcja sinus przyjmuje wartość –½ dwa razy w okresie, w szczególności dla – ^π⁄₆ oraz dla π – (– ^π⁄₆) .

Uwzględniając okresowość tej funkcji, rozwiązaniem są liczby postaci