Korzystamy ze wzoru na cosinus podwojonego kąta i otrzymujemy nierówność równoważną nierówności z zadania:

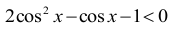
Podstawiamy t = cos x i rozwiązujemy nierówność kwadratową

2t² – t – 1 < 0

Miejscami zerowymi trójmianu 2t² – t – 1 są liczby t₁ = – ½ oraz t₂ = 1, zatem nierówność jest spełniona dla t ∈ (– ½, 1) czyli dla takich x, dla których – ½ < cos x < 1.

Poszukamy najpierw rozwiązań w przedziale ⟨ – π, π⟩.

Ponieważ

oraz funkcja cos jest rosnąca w przedziale ⟨ – π, 0⟩, to

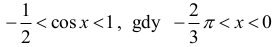
Podobnie,

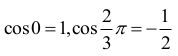
i funkcja cos jest malejąca w przedziale ⟨0, π⟩,

zatem

– ½ < cos x < 1 gdy 0 < x < ²⁄₃ π.

Pamiętając o okresowości funkcji cos, otrzymujemy ostatecznie rozwiązanie:

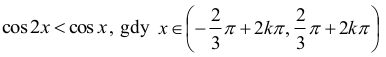
oraz x≠2kπ dla dowolnej liczby całkowitej k.