Równanie

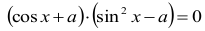
jest równoważne alternatywie

cos x + a = 0 (1)

lub

sin²x – a = 0 (2)

— Zauważmy, że dla a > 1 żadne z równań (1), (2) nie ma rozwiązania.

— Dla a = 1 równanie (1) przyjmuje postać cos x = – 1, a jego jedynym rozwiązaniem w przedziale ⟨0, 2π⟩ jest liczba π.

Z kolei równanie (2) przyjmuje postać sin²x = 1, czyli sin x = 1 lub sin x = –1. Rozwiązaniami w przedziale ⟨0, 2π⟩ są odpowiednio liczby:

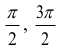
Zatem dla a = 1 mamy 3 rozwiązania.

— Dla a ∈ (0,1) równanie (2) przyjmuje postać sin²x = a, czyli sin x = √a lub sin x = –√a. Każde z równań sin x = √a oraz sin x = –√a ma w przedziale ⟨0, 2π⟩ dwa różne rozwiązania i żadne z rozwiązań równania sin x = √a nie może być rozwiązaniem równania sin x = –√a.

Zatem samo równanie (2) ma już 4 rozwiązania, co oznacza, że nie są spełnione warunki zadania.

— Dla dowolnej ujemnej wartości parametru a równanie sin²x – a = 0 nie ma rozwiązania. Z kolei równanie cos x + a = 0 może mieć w przedziale ⟨0, 2π⟩ co najwyżej 2 rozwiązania, zatem nie mogą być spełnione warunki zadania.

— Dla a = 0 mamy:

cos x = 0 lub sin²x = 0.