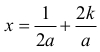
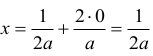
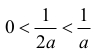
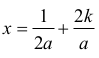
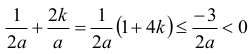
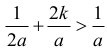
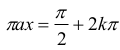
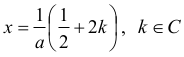
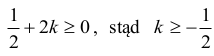
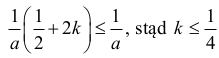
Zauważmy, że okresem zasadniczym funkcji sin(πax) jest liczba ²⁄_a i funkcja ta dokładnie jeden raz w okresie przyjmuje wartość 1, dla argumentu

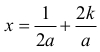
gdzie k jest dowolną liczbą całkowitą.

Dla k=0 mamy

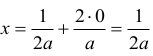
Widać, że

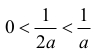
(ponieważ a>0, to otrzymane nierówności są równoważne nierównościom 0<½<1).

Pokażemy, że dla całkowitych wartości k≠0 liczby postaci

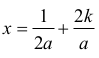
nie mieszczą się w przedziale ⟨0,¹⁄_a⟩.

Rzeczywiście, dla k<0 i a>0 mamy

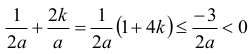
Z kolei dla k≥1 mamy

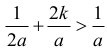
co jest równoważne nierówności ½ + 2k > 1 prawdziwej dla wszystkich liczb k>¼.

Zatem tylko dla k=0 spełnione są warunki zadania.

Ponieważ sin(πax)=1, to

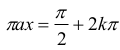
stąd

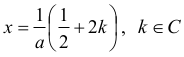
Ponieważ a>0 i musi być spełniony warunek x≥0, to

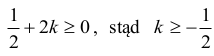
Ponadto musi być

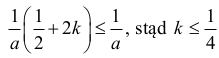
Po uwzględnieniu tego, że k jest liczbą całkowitą, otrzymujemy k=0