Odpowiedź:
Wyznaczamy wszystkie liczby spełniające równanie: sin x + sin 3x = 0 . Przekształcamy równanie równoważnie, korzystając ze wzoru na sumę sinusów: 2 sin 2x cos x = 0 . Równanie to jest spełnione, gdy sin 2x = 0 lub cos x = 0 , czyli dla x = kπ⁄2 , gdzie k jest liczbą całkowitą.
Najmniejszą liczbą dodatnią spełniającą równanie sin x + sin 3x = 0 jest x = π⁄2 .
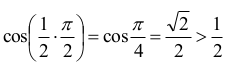
Z tego wynika, że dla x = π⁄2 nierówność
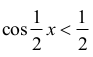
jest fałszywa.
Kolejną liczbą dodatnią spełniającą równanie sin x + sin 3x = 0 jest x = π .
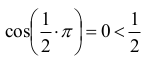
Z tego wynika, że dla x = π nierówność
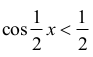
jest prawdziwa.
Najmniejszą liczbą dodatnią spełniającą warunki zadania jest x = π .