Odpowiedź:
I sposób
Funkcja ƒ ma postać
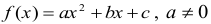
Wyznaczmy wzór funkcji g oraz wzór funkcji h.
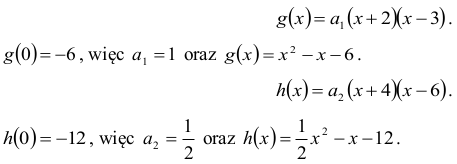
Wiemy, że
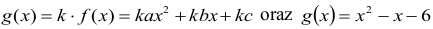
Wiemy również, że
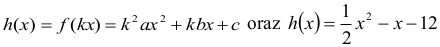
Wynika z tego, że a=2, b=-2 oraz c=-12
Tak więc ƒ(x) = 2x2 – 2x – 12
II sposób
Funkcja ƒ ma postać
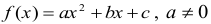
Wynika z tego, że
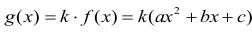
Miejscami zerowymi funkcji g są liczby x1 = -2 i x2 = 3 .
Tak więc
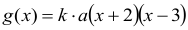
Z postaci funkcji ƒ i g wynika, że liczby x1 = -2 i x2 = 3 są również miejscami zerowymi funkcji ƒ i ƒ(x) =a(x + 2)(x – 3) .
Funkcja h ma postać
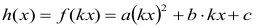
Zauważmy, że wyraz wolny "c" nie jest zależny od k. Oznacza to, że dla funkcji ƒ oraz funkcji
h wartość c jest taka sama i wynosi c = -12 .
Wiemy, że c = ƒ(0) = -12. Tak więc punkt (0, -12) należy do wykresu funkcji ƒ.
Określiliśmy funkcję f wzorem:
Po podstawieniu punktu (0, -12) do wzoru funkcji otrzymamy wartość współczynnika a:
a(0 + 2)(0 – 3) = –12
–6a = –12
a = 2
Funkcja f ma postać
Po przekształceniu wzoru do postaci ogólnej mamy
f(x) = 2x2 – 2x – 12