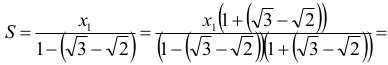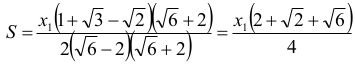Odpowiedź:
Wprowadzamy oznaczenia:
d — przekątna sześcianu,
k — przekątna ściany sześcianu.
Ponieważ krawędź wyjściowego sześcianu jest równa x1, zatem
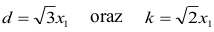
Krawędź drugiego sześcianu jest równa:
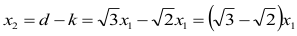
Długości krawędzi kolejnych sześcianów tworzą nieskończony ciąg geometryczny (xn), w którym x1 jest pierwszym wyrazem, natomiast
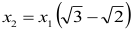
Stąd

Spełniony jest warunek zbieżności |q|<1 .
Obliczamy sumę S = x1 + x2 + x3 +... długości krawędzi tak powstałych sześcianów: