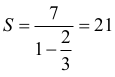Odpowiedź:
Ponieważ ciąg (an) jest geometryczny, jego wzór ogólny ma postać an = 7·qn–1 dla n ∈ {1,2,3,...} . Zauważmy, że q≠0, gdyż w przeciwnym razie w równaniu rekurencyjnym dojdzie do sprzeczności dla n = 1 .
Podstawiamy wyraz ogólny do wzoru rekurencyjnego:
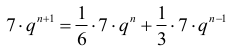
Podzielmy równanie przez 7·qn–1 . Otrzymujemy równanie
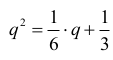
stąd
6q2 – q – 2 = 0
Obliczamy wyróżnik: Δ = 1+4·2·6=49
stąd
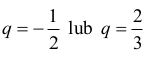
Zatem ciąg (an) ma postać:
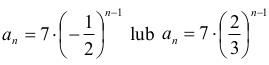
Gdy ciąg (an) ma postać:
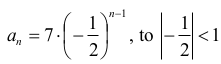
więc suma wszystkich wyrazów ciągu (an) jest równa
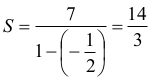
Gdy ciąg (an) ma postać:
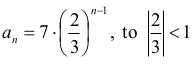
więc suma wszystkich wyrazów ciągu (an) jest równa