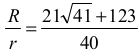Odpowiedź:
I sposób

Wprowadzamy oznaczenia jak na rysunku:

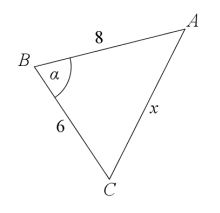
Korzystamy z jedynki trygonometrycznej:


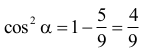
Rozpatrujemy dwa przypadki


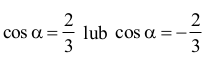
Wykorzystujemy twierdzenie cosinusów do wyznaczenia boku |AC| = x.

I. Dla cos α = 2⁄3 otrzymujemy:


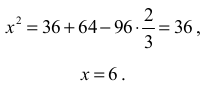
Z twierdzenia sinusów otrzymujemy:


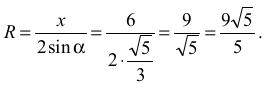
Obliczamy pole trójkąta i jego obwód:


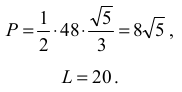
Obliczamy promień okręgu wpisanego:


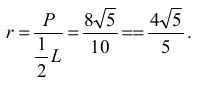
Wyznaczamy stosunek promieni:



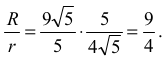
II. Dla cos α = – 2⁄3 otrzymujemy:


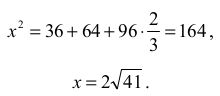
Z twierdzenia sinusów otrzymujemy:


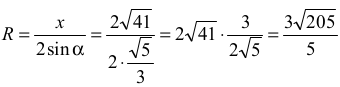
Obliczamy obwód trójkąta:


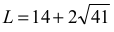
Obliczamy promień okręgu wpisanego:


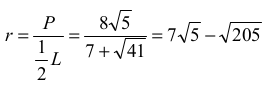
Wyznaczamy stosunek promieni:


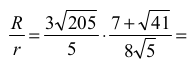
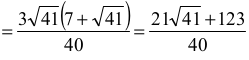
Dla trójkąta ostrokątnego


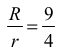
natomiast dla rozwartokątnego



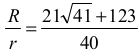
II sposób

Korzystamy z jedynki trygonometrycznej:


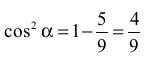
Rozpatrujemy dwa przypadki:


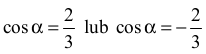
Wykorzystujemy twierdzenie cosinusów do wyznaczenia boku |AC| = x.

Dla cos α = 2⁄3 otrzymujemy:


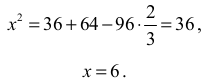
Obliczamy pole trójkąta i połowę jego obwodu:





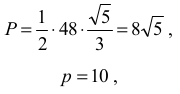
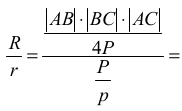
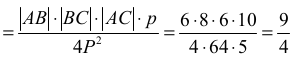
Dla cos α = – 2⁄3 otrzymujemy:


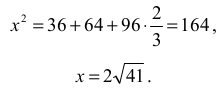
Obliczamy połowę obwodu trójkąta:

p = 7 + √41,



Dla trójkąta ostrokątnego


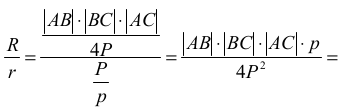
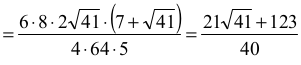
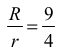
natomiast dla rozwartokątnego

Powrót do pytań