Obwód trapezu L wyraża się wzorem L = a + b + 2c.

Trapez jest opisany na okręgu, więc sumy długości jego przeciwległych boków są równe.

Oznacza to, że a + b = 2c. Wynika z tego, że L = 4c.

Wyznaczmy długość boku c.

Wiemy, że promień okręgu

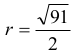
Tak więc wysokość trapezu

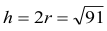
Rozważmy trójkąt o bokach długości x, h i c, gdzie

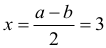
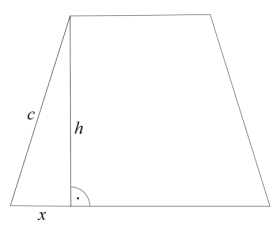
Z twierdzenia Pitagorasa mamy

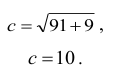
Wynika z tego, że obwód trapezu L = 40.

Obwód trapezu L wyraża się wzorem L = a + b + 2c.

Trapez jest opisany na okręgu, więc sumy długości jego przeciwległych boków są równe.

Oznacza to, że a + b = 2c. Wynika z tego, że L = 2(a + b).

Wiemy, że a – b = 6. Wyznaczmy długość boku b.

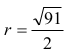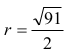Zauważmy, że CSB jest trójkątem prostokątnym oraz jest wysokością tego trójkąta.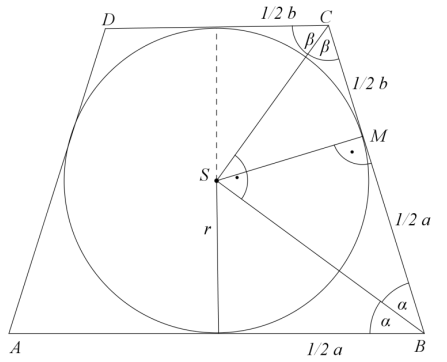

wtedy

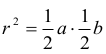
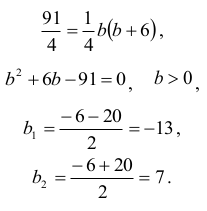
Tak więc b = 7 .

Oznacza to, że L = 2(2 · 7 + 6) = 40.