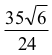Odpowiedź:
Oznaczmy:
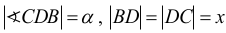
Ponieważ trójkąt CDB jest równoramienny i |BD| = |DC|
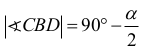
Kąty DBC i DAC są wpisane w okrąg i oparte na tym samym łuku DC, więc
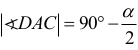
Kąty CDB i CAB są wpisane w okrąg i oparte na tym samym łuku BC, więc |∢CAB| = α .
Korzystamy z twierdzenia cosinusów w trójkącie DAC:
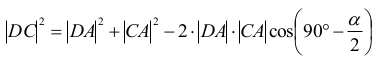
zatem
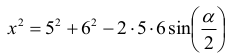
Korzystamy z twierdzenia cosinusów w trójkącie DAB:
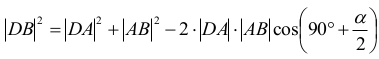
zatem
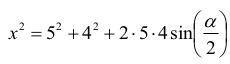
Tworzymy układ równań:
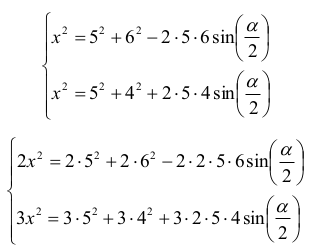
Dodając równania stronami, otrzymujemy:
5x2 = 5·52 + 3·42 + 2·62
x2 = 49
x = 7
Wówczas:
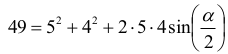
a więc
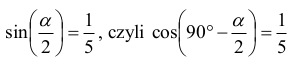
Z tożsamości sin2 α + cos2 α = 1 otrzymujemy
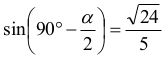
Z twierdzenia sinusów otrzymujemy:
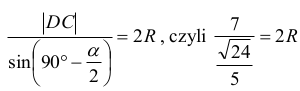
Promień okręgu opisanego na czworokącie ma długość: