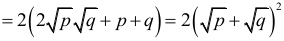Oznaczmy przez Q i R odpowiednie punkty styczności (zobacz rysunek).

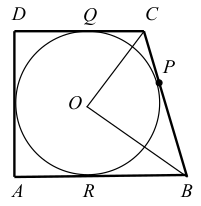
Wówczas odcinki OC i OB zawierają się w dwusiecznych kątów ABC i BCD, a ponieważ suma tych kątów jest równa 180 stopni, więc kąt BOC jest prosty.

W trójkącie prostokątnym BOC spełniony jest warunek |OP|² = pq (wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na dwa takie odcinki, że iloczyn ich długości jest równy kwadratowi tej wysokości). Ale OP jest równa promieniowi okręgu, zatem

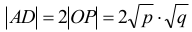
Z własności czworokąta opisanego na okręgu otrzymujemy, że

zatem

= 2(|AD| + |CB|) =