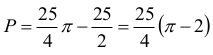Odpowiedź:
I sposób
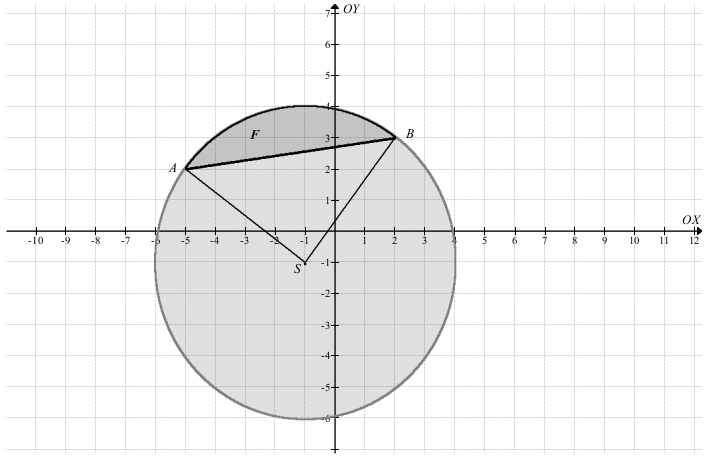
Figura F jest ograniczona prostą
oraz łukiem okręgu
(x + 1)2 + (y + 1)2 = 25
o środku S = (–1,–1) i promieniu r = 5 .
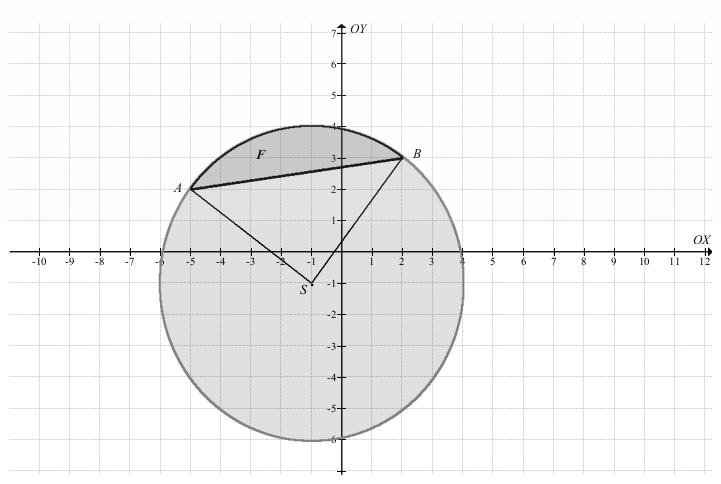
Punktami wspólnymi prostej i okręgu są punkty A = (–5,2) i B = (2,3) :
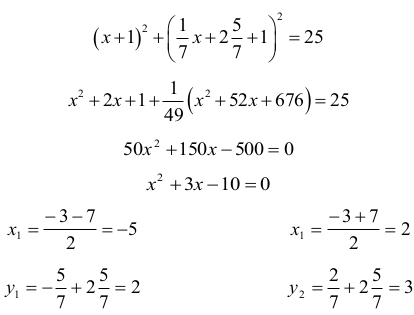
Zauważmy, że pole P figury F jest równe różnicy pola PW wycinka kołowego o promieniu r
i kącie ASB oraz pola PT trójkąta równoramiennego ASB.
P = PW – PT
Przyjmijmy, że kąt ASB ma miarę α.
Pole wycinka kołowego wyraża się wzorem:
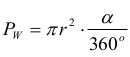
W tym miejscu wystarczy zauważyć, że trójkąty AA'S i BB'S, gdzie A'=(–5,–1), B'=(2,–1), to przystające trójkąty prostokątne (o bokach 3, 4, 5), więc z uzupełniania kątów przy wierzchołku S, kąt α jest prosty.
Kąt α = 90°, tak więc
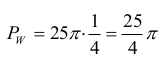
Obliczmy teraz długość odcinka AB:
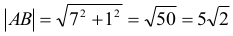
Trójkąt ASB jest prostokątny i równoramienny, więc jego pole jest równe
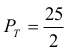
Z powyższego wynika, że pole figury F jest równe:
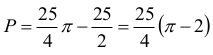
II sposób
Figurę F wyznaczają koło o środku S = (–1,–1) i promieniu r = 5 oraz prosta y = 1⁄7 x + 2 5⁄7
Zauważmy, że pole P figury F jest równe różnicy pola PW wycinka kołowego o promieniu r
i kącie ASB oraz pola PT trójkąta równoramiennego ASB.
P = PW – PT
Przyjmijmy, że kąt ASB ma miarę α.
Pole wycinka kołowego wyraża się wzorem:
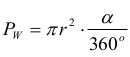
Wyznaczmy odległość punktu S = (–1,–1) od prostej y = 1⁄7 x + 2 5⁄7
Przekształćmy równanie prostej do postaci ogólnej:
x – 7y + 19 = 0
Odległość punktu S od danej prostej jest równa:
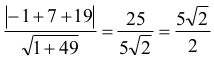
Zauważmy, że dana odległość jest połową długości przekątnej kwadratu o boku |AS| = |AB| = 5.
Oznacza to, że α = 90° .
Tak więc
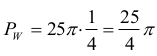
Trójkąt ASB jest prostokątny i równoramienny, więc jego pole jest równe
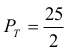
Pole figury F jest więc równe: