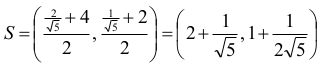Odpowiedź:
I sposób
Z równań tych okręgów wnioskujemy, że okrąg o1 ma środek w punkcie (0,0) i promień
równy 1, natomiast okrąg o2 ma środek w punkcie (6,3) i promień równy √5, zatem odległość między tymi środkami jest równa
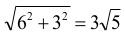
(tak więc okręgi nie mają punktów wspólnych), natomiast
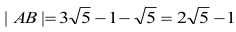
Wynika stąd, że odległość środka S odcinka AB od punktu (0,0) jest równa
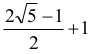
czyli
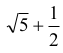
Jednocześnie S leży na prostej przechodzącej przez oba środki okręgów, czyli na prostej o równaniu y = ½ x , zatem jego współrzędne mają postać (x, ½ x) . Otrzymujemy stąd równanie
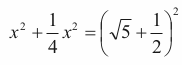
które po przekształceniach przybiera postać
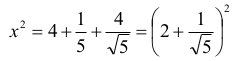
Punkt S leży w pierwszej ćwiartce układu współrzędnych, zatem jego współrzędnymi są
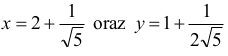
II sposób
Z równań tych okręgów wnioskujemy, że okrąg o 1 ma środek w punkcie (0,0) , natomiast
okrąg o 2 ma środek w punkcie (6,3). Odcinek łączący punkty A i B leży na prostej przechodzącej przez te dwa punkty, wyznaczamy więc równanie tej prostej:
y = ½ x
Punkt A jest wspólny dla tej prostej i okręgu o 1 , musi zatem spełniać układ równań
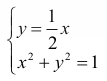
lub — równoważnie — układ
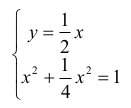
czyli
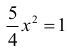
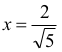 i w konsekwencji
i w konsekwencji 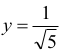
Tak więc
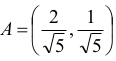
Podobnie wyznaczamy współrzędne punktu B, rozwiązując układ równań
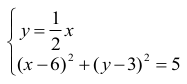
prowadzący do równania kwadratowego
x2 – 12x + 32 = 0
którego pierwiastkami są liczby 8
i 4. Pierwsze z tych rozwiązań odrzucamy, gdyż żaden punkt o pierwszej współrzędnej 8 nie
należy do odcinka łączącego punkty (0,0) i (6,3). Pozostaje zatem x = 4 i w konsekwencji
y = 2 . Tak więc B = (4,2) .
Teraz możemy wyznaczyć środek S odcinka AB :