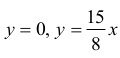Odpowiedź:
I sposób
Naszkicujmy rysunek w układzie współrzędnych.

Zauważmy, że prosta x = 0 nie jest styczną, zatem każdą ze stycznych da się opisać równaniem
ax – y = 0
Odległość każdej ze stycznych od punktu S jest równa 3, zatem

Stąd otrzymujemy kolejno:
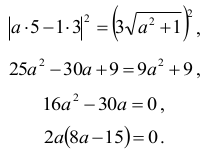
Stąd
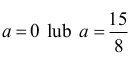
Styczne mają równania:
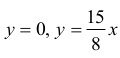
II sposób
Naszkicujmy rysunek w układzie współrzędnych.
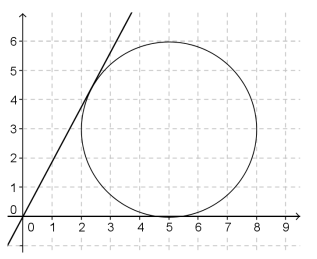
Zauważmy, że prosta x = 0 nie jest styczną, zatem każdą ze stycznych da się opisać równaniem y = ax.
Zapiszmy układ równań prowadzący do wyznaczenia punktów wspólnych prostej i okręgu:

Po podstawieniu i uporządkowaniu otrzymujemy równanie kwadratowe jednej zmiennej:
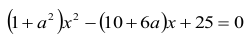
Okrąg ma ze styczną jeden punkt wspólny, tym samym równanie ma mieć jedno rozwiązanie, zatem wyróżnik otrzymanego trójmianu musi być równy 0, czyli:
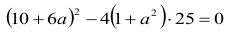
Po odpowiednim rozwinięciu i redukcji wyrazów podobnych otrzymujemy:
8a(15 – 8a) = 0
Stąd
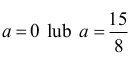
Styczne mają równania: