Odpowiedź:
Trójkąt ABC jest prostokątny i równoramienny. Pole tego trójkąta jest równe
PABC = ½·4·4 = 8
Zauważmy najpierw, że jeśli okrąg o środku C dzieli trójkąt na dwie figury o równych polach,
to promień tego okręgu jest mniejszy od przyprostokątnej trójkąta. Gdyby był większy, to
wtedy pole części „wykrojonej” z trójkąta przez okrąg byłoby co najmniej równe polu wycinka koła o kącie 45° i promieniu 4, więc co najmniej równe
1⁄8·π·42 = 2π
Byłoby więc większe od połowy pola trójkąta. W rezultacie okrąg dzieli trójkąt na dwie figury, z których jedną
jest wycinek koła o promieniu r i kącie 45°. Pole tego wycinka jest równe 4.
Wynika stąd, że całe koło ma pole równe 8·4 = 32. Ze wzoru na pole koła otrzymujemy 32 = πr2, skąd
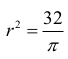
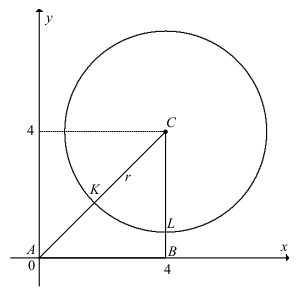
Ponieważ punkt C = (4,4) jest środkiem okręgu, to równanie tego okręgu ma postać
(x – 4)2 + (y – 4)2 = r2
a więc szukany okrąg ma równanie
(x – 4)2 + (y – 4)2 = 32⁄π