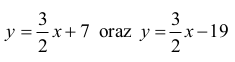Zauważmy, że odcinki KL i KM są przyprostokątnymi rozważanego trójkąta.

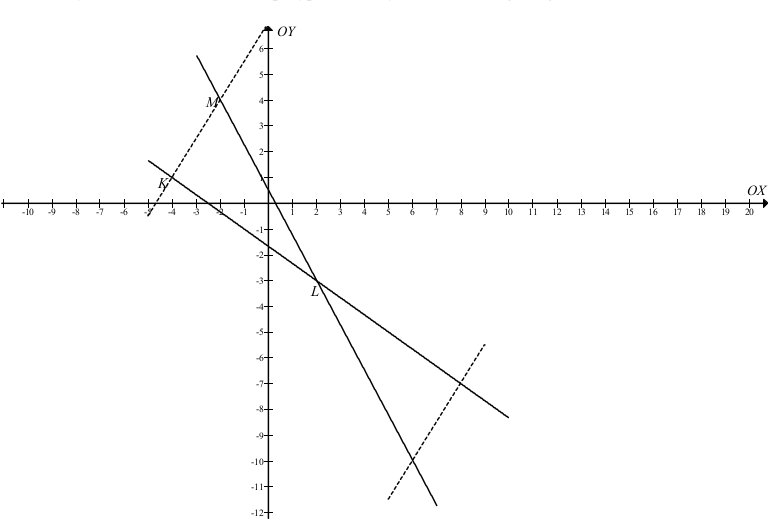
Prosta KM jest prostopadła do prostej KL i przechodzi przez punkt K.

Pole trójkąta KLM określone jest wzorem

P = ½ |KL|·|KM|.

Długość odcinka KL jest odległością punktu L od prostej KM oraz |KM| jest odległością punktu M od prostej KL o równaniu

2x + 3y + 5 = 0.

Zauważmy, że prosta KM jest prostopadła do prostej KL:

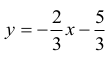
KM ma więc postać

y = ³⁄₂ x + b

Po przekształceniu równania do postaci ogólnej mamy:

3x – 2y + 2b = 0

Wyznaczmy teraz współrzędne punktu L:

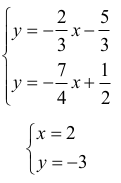
Tak więc L = (2,–3).

Odległość punktu L od prostej KM jest równa

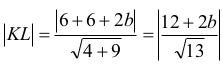
Określmy teraz współrzędne punktu M.

M jest punktem przecięcia prostych:

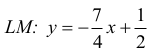
oraz prostej

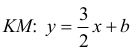
Drugą współrzędną punktu M można wyrazić na dwa sposoby:

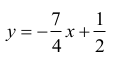
oraz

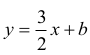
Możemy więc zapisać:

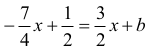
Tak więc

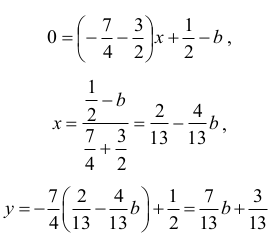
Punkt M ma więc współrzędne

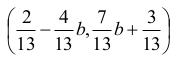
Wyznaczmy odległość punktu M od prostej KL: 2x + 3y + 5 = 0

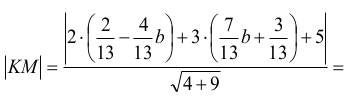
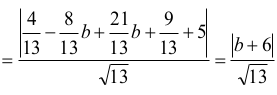
Pole trójkąta KLM dane jest więc wzorem:

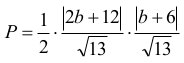
Wynika z tego, że

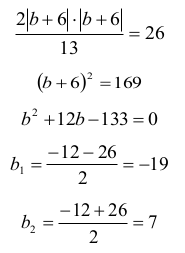
Tak więc prosta KM określona jest następującymi równaniami: