Z warunku prostopadłości prostych wynika, że

a·(2b – 1) = b·(–a) = 0

Możemy zapisać równanie

a[(2b – 1) – b] = 0

które jest równoważne alternatywie:

a = 0 ∨ b = 1

Ale z treści zadania mamy, że a>0

Dla b = 1 równania prostych przyjmują postać:

k: ax + y – 4a = 0

l: x – ay  – 4 = 0

Niech A oraz B będą punktami wspólnymi prostych odpowiednio k i l z osią Oy. Wtedy

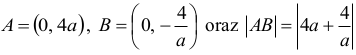
Trzeci wierzchołek trójkąta jest punktem wspólnym prostych k i l, zatem jego współrzędne wyznaczymy, rozwiązując układ równań

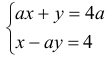
Mnożąc drugie z równań przez liczbę –a i dodając równania stronami, otrzymujemy warunek

(a² + 1)y = 0

Ostatnia równość jest spełniona tylko dla y = 0. Wtedy x = 4.

Widać więc, że wysokość poprowadzona na bok AB ma długość 4. Prowadzi to do równania

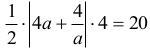
które, korzystając z faktu, że a jest liczbą dodatnią, możemy zapisać w postaci równoważnej

2a² – 5a +2 = 0

Jego rozwiązaniami są liczby

a = 2 lub a = ½