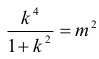Odpowiedź:
I sposób
Aby wyznaczyć punkty wspólne prostej i okręgu, rozwiążemy układ równań.
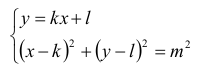
Okrąg i prosta mają jeden punkt wspólny, gdy układ równań posiada jedno rozwiązanie:
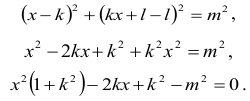
Równanie kwadratowe z niewiadomą x posiada jedno rozwiązanie, gdy
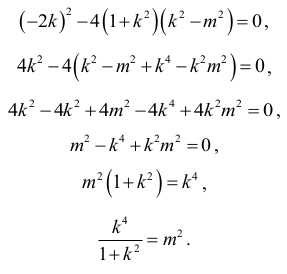
Tak więc, jeśli prosta jest styczna do okręgu, to zachodzi równość
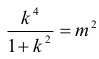
II sposób
Prosta y = kx + l i okrąg (x – k)2 + (y – l)2 = m2 są styczne, gdy odległość d między prostą i środkiem okręgu S = (k,l) jest równa długości promienia m.
Wyznaczmy odległość punktu S = (k,l) od prostej o równaniu kx – y + l = 0 .
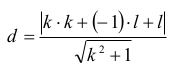
Prosta i okrąg mają jeden punkt wspólny, gdy d = m:
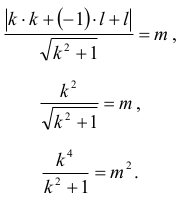
Tak więc jeśli prosta jest styczna do okręgu, to zachodzi równość