Odpowiedź:
I sposób
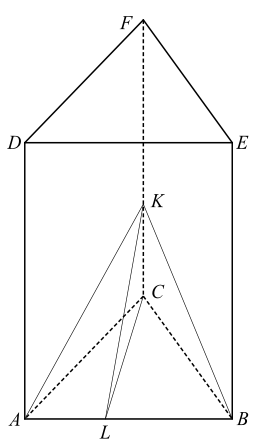
Wprowadzamy oznaczenia jak na rysunku:
L — środek krawędzi AB.
L — środek krawędzi AB.
Obliczamy wysokość podstawy graniastosłupa:
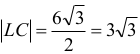
Przekrój graniastosłupa opisaną płaszczyzną jest trójkątem równoramiennym ABK o polu 15√3, zatem otrzymujemy:
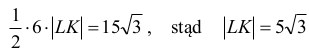
Stosujemy twierdzenie Pitagorasa dla trójkąta LCK:
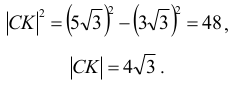
Rozpatrujemy dwie sytuacje.
Sytuacja pierwsza:
odcinek
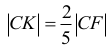
zatem
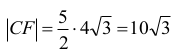
Obliczamy objętość graniastosłupa:
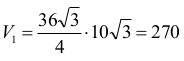
Sytuacja druga:
odcinek
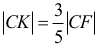
zatem
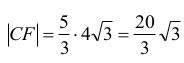
Obliczamy objętość graniastosłupa:
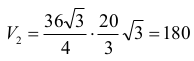
Objętość graniastosłupa jest równa 180 lub 270.
II sposób
Korzystamy z oznaczeń na rysunku w I sposobie.
Niech x = |AK| = |BK|
Przekrój graniastosłupa opisaną płaszczyzną jest trójkątem równoramiennym ABK.
Obwód trójkąta ABK jest opisany wyrażeniem 2x + 6, a jego pole jest równe 15√3.
Wykorzystujemy wzór Herona:
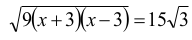
stąd x = √84 = 2√21.
Stosujemy twierdzenie Pitagorasa dla trójkąta BCK:
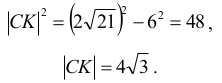
Rozpatrujemy dwie sytuacje.
Dalsza część zadania tak, jak w I sposobie.