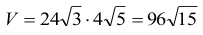Odpowiedź:
Przekrój graniastosłupa prawidłowego sześciokątnego jest sześciokątem wypukłym, składającym się z dwóch przystających trapezów równoramiennych.
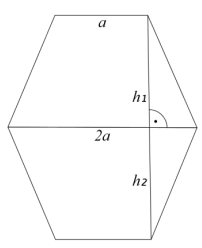
Podstawy trapezów mają długości a i 2a.
Oznaczmy wysokość trapezów jako h1 i h2 (trapezy są przystające, więc h1 = h2 = h).
Pole danego przekroju jest więc równe:
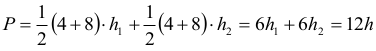
Tak więc
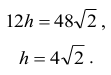
Objętość graniastosłupa dana jest wzorem:
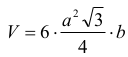
gdzie a jest długością krawędzi podstawy, a b jest długością krawędzi bocznej graniastosłupa. Wiemy, że a = 4 , tak więc
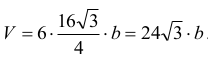
Wyznaczmy długość b.
Zauważmy, że odcinek b jest przyprostokątną trójkąta, którego druga przyprostokątna x, jest równa
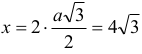
Przeciwprostokątna tego trójkąta ma długość
2h = 8√2
Tak więc
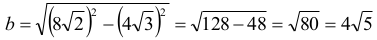
Wyznaczmy teraz objętość graniastosłupa: