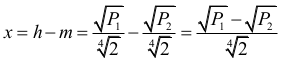Odpowiedź:
I sposób
Ponieważ płaszczyzny ABC i DEF są równoległe, a
płaszczyzna ABC jest prostopadła do krawędzi AS,
to odległość między tymi płaszczyznami stanowi
długość odcinka AD. Oznaczmy ją literą x. Przyjmijmy też oznaczenia jak na rysunku.
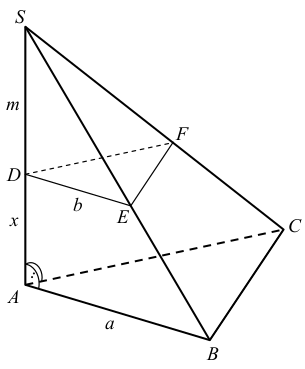
Zauważmy, że trójkąty ABC i DEF są jednokładne.
Jeden
z
nich
jest
obrazem
drugiego
w jednokładności o środku S, np. trójkąt DEF jest
obrazem trójkąta ABC w jednokładności o środku S i skali
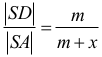
Zatem trójkąt DEF jest również podobny do trójkąta ABC w tej samej skali.
Stosunek pól trójkątów podobnych jest równy
kwadratowi skali ich podobieństwa, więc
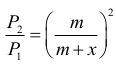
Stąd otrzymujemy
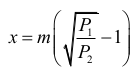
Trójkąty SDE i SDF są przystające i każdy z nich jest „połową” trójkąta równobocznego o wysokości b i boku długości |SE| = 2m. Zatem
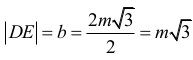
Trójkąt SEF jest równoboczny, więc |EF| = |SE| = 2m. Trójkąt DEF jest równoramienny. Wysokość h tego trójkąta poprowadzona z wierzchołka D jest równa
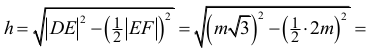
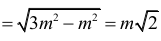
więc jego pole P2 jest równe
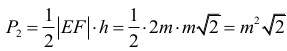
sąd
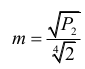
Po uwzględnieniu
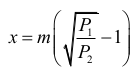
otrzymujemy
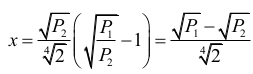
II sposób
Ponieważ płaszczyzny ABC i DEF są równoległe, a płaszczyzna ABC jest prostopadła do
krawędzi AS, to odległość między tymi płaszczyznami stanowi długość odcinka AD.
Oznaczmy ją literą x. Przyjmijmy też oznaczenia jak na rysunku.
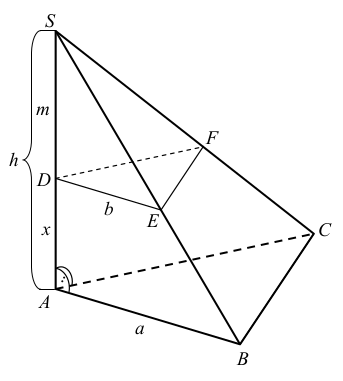
Trójkąty SAB i SAC prostokątne, gdyż krawędź
boczna AS jest wysokością ostrosłupa opuszczoną na podstawę ABC. Krawędź ta jest
wspólną przyprostokątną tych trójkątów. Ponadto |∠ASB| = |∠ASC| = 60° . Zatem trójkąty
nadto
SAB i SAC są przystające i każdy z nich jest
„połową” trójkąta równobocznego o wysokości
a i boku długości |SB| = 2h . Zatem
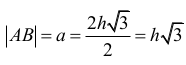
W trójkącie SBC krawędzie BS i CS mają tę samą długość, co wynika z przystawania trójkątów SAB i SAC. Ponadto |∠BSC| = 60° , więc trójkąt SBC jest równoboczny. Zatem |BC| = |SB| = 2h . Trójkąt ABC jest równoramienny. Wysokość p tego trójkąta poprowadzona z wierzchołka A jest równa
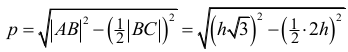
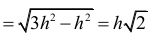
więc jego pole P1 jest równe
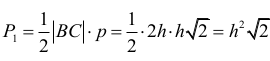
skąd
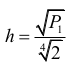
Analogicznie zauważamy, że trójkąty SDE i SDF są przystające i każdy z nich jest „połową”
trójkąta równobocznego o wysokości b i boku długości |SE| = 2m. Powtarzając analogiczne
obliczenia, otrzymujemy
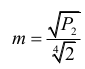
Zatem szukana odległość x jest równa