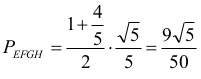Odpowiedź:
Zauważmy, że zarówno otrzymany przekrój EFGH,
jak i czworokąt BCGH są trapezami o takich samych podstawach i różnych wysokościach. Poprowadźmy z wierzchołka H wysokości HQ i HP odpowiednich trapezów.
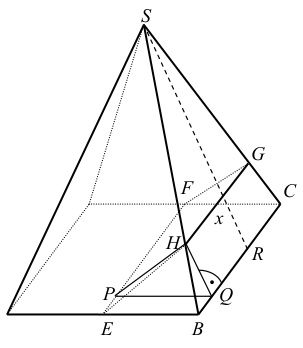
Przyjmijmy oznaczenia:
|GH| = x
|HP| = p
|HQ| = q
Oczywiście x ∈ (0,1)
wtedy
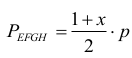
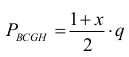
Stosunek pól obu trapezów jest więc równy:
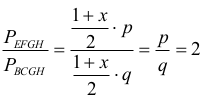
Oznaczmy przez h wysokość SR ściany bocznej. Z twierdzenia Pitagorasa wynika, że wtedy
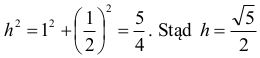
Trójkąty BHQ i BSR są podobne, zatem w szczególności
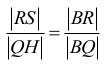
co przy przyjętych oznaczeniach można wyrazić w postaci:
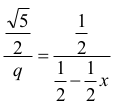
zatem
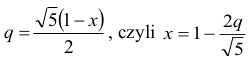
Kąt PQH jest równy kątowi nachylenia ściany bocznej do płaszczyzny podstawy, bo odcinki HQ i PQ są prostopadłe do prostej BC. Zatem jego cosinus jest równy:
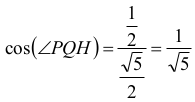
Korzystając z twierdzenia cosinusów (dla trójkąta PQH), możemy zapisać, że
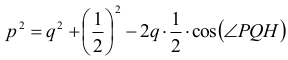
czyli
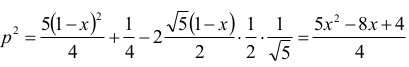
Ponieważ
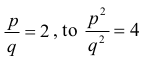
Otrzymujemy zatem równanie z niewiadomą x:
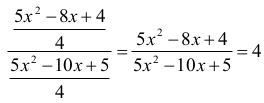
czyli
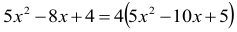
Po redukcji otrzymujemy równanie kwadratowe
15x2 – 32x + 16 = 0
Ponieważ Δ = 64, to
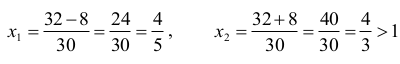
zatem
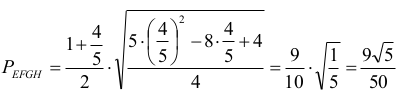
Uwaga
Ostatni etap rozwiązania można przeprowadzić dla zmiennych p, q, a dopiero później obliczyć x.
Ponieważ
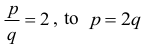
Stąd, z równania
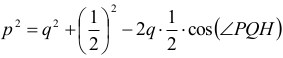
otrzymujemy równanie z niewiadomą q:
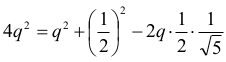
które po uporządkowaniu przyjmuje postać:
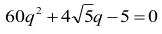
Ponieważ
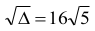
to
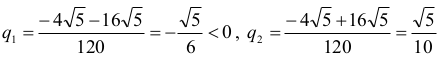
zatem
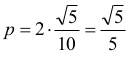
oraz
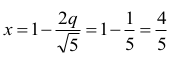
stąd