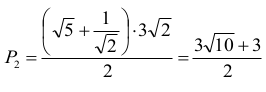Odpowiedź:
Przykładowe rozwiązanie
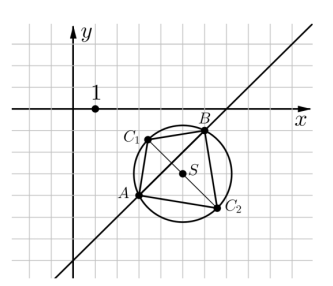
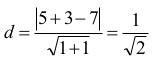
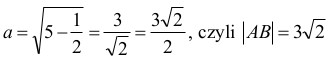
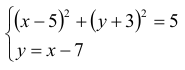
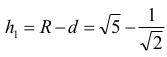
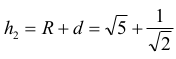
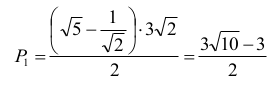
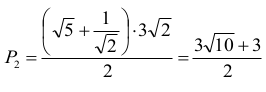
Środkiem okręgu (x – 5)2 + (y + 3)2 = 5 jest punkt S = (5, –3) , natomiast promień R = √5 .
W okrąg można wpisać dwa trójkąty równoramienne ABC1 i ABC2 , których podstawą jest odcinek AB (zobacz rysunek).

Obliczamy odległość d środka S od prostej o równaniu x – y – 7 = 0 :
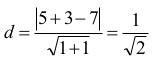
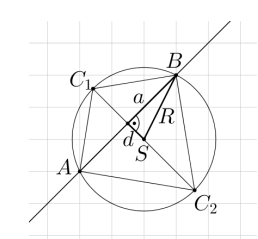
Oznaczmy przez a = ½ |AB| (zobacz rysunek)

Z twierdzenia Pitagorasa możemy zapisać:
a2 + d2 = R2
zatem
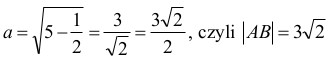
Uwaga
Długość odcinka AB możemy też obliczyć, wyznaczając najpierw współrzędne punktów przecięcia danej prostej i okręgu. Wystarczy rozwiązać układ równań:
Długość odcinka AB możemy też obliczyć, wyznaczając najpierw współrzędne punktów przecięcia danej prostej i okręgu. Wystarczy rozwiązać układ równań:
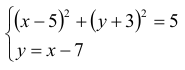
Wysokość trójkąta ABC1 poprowadzona z wierzchołka C1 jest równa
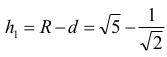
Wysokość trójkąta ABC2 poprowadzona z wierzchołka C2 jest równa
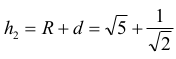
Z tego wynika, że pole trójkąta ABC1:
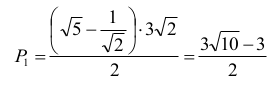
oraz pole trójkąta ABC2: