Niech Ω={(x,y):x,y∈{1,2,3,4,5,6}}, zatem |Ω| = 36.

Niech A będzie zdarzeniem: suma kwadratów wyrzuconych liczb przy dzieleniu przez 4 daje resztę 1. Niech B będzie zdarzeniem: wartość bezwzględna różnicy wyrzuconych liczb będzie większa od 2.

Skorzystamy z prawdopodobieństwa warunkowego:

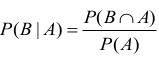
Ponieważ suma kwadratów wyrzuconych liczb przy dzieleniu przez 4 daje resztę 1, wyrzucono jedną liczbę parzystą i jedną nieparzystą. Zatem |A| = 18.

Zdarzenie B ∩ A oznacza, że jedna liczba jest parzysta, druga nieparzysta i wartość bezwzględna różnicy wyrzuconych liczb jest większa od 2.

Wobec tego mamy następujące pary:

(1,4), (1,6), (2,5), (3,6), (4,1), (5,2), (6,1), (6,3)

czyli |B ∩ A| = 8

zatem