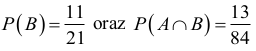Odpowiedź:
I sposób
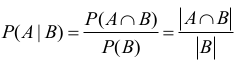
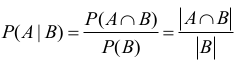
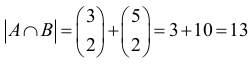
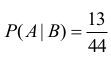
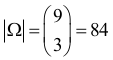
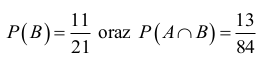
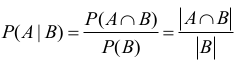
|B| = 4·3·2 + 3·4·5·4 = 264
|A ∩ B| = 3·3·2 + 3·5·4 = 78
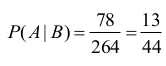
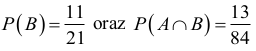
Zdarzeniami elementarnymi są wszystkie trójelementowe podzbiory (kombinacje) zbioru {1,2,...,9}. Jest to model klasyczny.
Wprowadzamy oznaczenia dla zdarzeń:
A — wśród wylosowanych liczb będzie liczba 4,
A — wśród wylosowanych liczb będzie liczba 4,
B — suma wylosowanych liczb będzie parzysta.
Mamy obliczyć
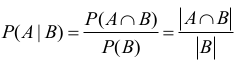
Zdarzeniu B sprzyjają podzbiory trójelementowe złożone z trzech liczb parzystych albo złożone z jednej liczby parzystej i dwóch nieparzystych:
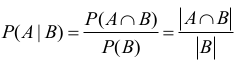
Zdarzeniu A ∩ B sprzyjają podzbiory trójelementowe złożone z liczby 4 i dwóch liczb parzystych albo złożone z liczby 4 i dwóch liczb nieparzystych:
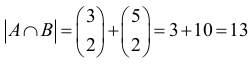
stąd
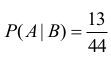
Uwaga: Możesz obliczyć
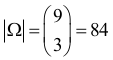
następnie
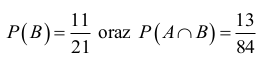
II sposób
Zdarzeniami elementarnymi są wszystkie trójwyrazowe wariacje bez powtórzeń zbioru {1,2,...,9}. Jest to model klasyczny.
Wprowadzamy oznaczenia dla zdarzeń:
A — wśród wylosowanych liczb będzie liczba 4,
A — wśród wylosowanych liczb będzie liczba 4,
B — suma wylosowanych liczb będzie parzysta.
Mamy obliczyć
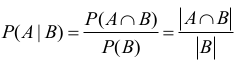
Zdarzeniu B sprzyjają wariacje bez powtórzeń, których wyrazami są trzy liczby parzyste albo jedna liczba parzysta i dwie nieparzyste,
Zdarzeniu A ∩ B sprzyjają trójwyrazowe wariacje bez powtórzeń, w których występuje liczba 4 i dwie liczby parzyste albo liczba 4 i dwie liczby nieparzyste:
stąd
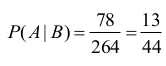
Uwaga: Możesz obliczyć |Ω| = 9·8·7 = 504 , następnie