Odpowiedź:
I sposób
Zacznijmy od wybrania dowolnej cyfry różnej od zera. Możemy to zrobić na 9 sposobów. Umieśćmy wybraną cyfrę (nazwijmy ją a) na miejscu setek. Teraz — znów na 9 sposobów — wybieramy drugą cyfrę, różną od a; nazwijmy ją b.
Jak możemy wypełnić miejsca dziesiątek i jedności? Pierwszy sposób: na obu tych miejscach wpisujemy b. Drugi sposób: na miejscu dziesiątek wpisujemy b, na miejscu zaś jedności wpisujemy a. Trzeci sposób: na miejscu dziesiątek wpisujemy a, na miejscu jedności wpisujemy b. Tak więc dla każdego z 9 sposobów wyboru cyfry b mamy 3 sposoby utworzenia liczby trzycyfrowej spełniającej warunki zadania.
W ten sposób z zasady mnożenia otrzymujemy odpowiedź: 9·9·3=243
II sposób
Zgodnie z warunkami zadania interesują nas liczby, w których zapisie dziesiętnym jedna cyfra występuje dokładnie dwa razy, inna — dokładnie raz. Niech a oznacza niezerową cyfrę. Może ona wystąpić dwukrotnie w zapisie liczby trzycyfrowej na 3 sposoby
liczba kombinacji
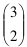
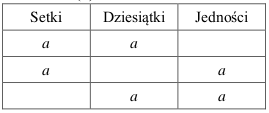
Puste pozycje dziesiątek i jedności możemy wypełnić na 9 sposobów, bo tyle jest cyfr różnych od a. Z kolei pozycję setek możemy wypełnić tylko na 8 sposobów, gdyż nie możemy tam wpisać cyfry 0. Ponieważ mamy 9 możliwych wartości a, łącznie mamy 2·9·9+9·8, czyli 234 liczby o powtarzającej się cyfrze różnej od 0 (reguła mnożenia, następnie reguła dodawania).
Para 0-0 może wystąpić tylko w jeden sposób, jako że 0 nie może wystąpić na pozycji setek, na której może jej towarzyszyć dowolna cyfra niezerowa; mamy zatem 9 możliwości. Łącznie mamy więc 234 + 9, czyli 243 liczby spełniające warunki zadania.
Zacznijmy od wybrania dowolnej cyfry różnej od zera. Możemy to zrobić na 9 sposobów. Umieśćmy wybraną cyfrę (nazwijmy ją a) na miejscu setek. Teraz — znów na 9 sposobów — wybieramy drugą cyfrę, różną od a; nazwijmy ją b.
Jak możemy wypełnić miejsca dziesiątek i jedności? Pierwszy sposób: na obu tych miejscach wpisujemy b. Drugi sposób: na miejscu dziesiątek wpisujemy b, na miejscu zaś jedności wpisujemy a. Trzeci sposób: na miejscu dziesiątek wpisujemy a, na miejscu jedności wpisujemy b. Tak więc dla każdego z 9 sposobów wyboru cyfry b mamy 3 sposoby utworzenia liczby trzycyfrowej spełniającej warunki zadania.
W ten sposób z zasady mnożenia otrzymujemy odpowiedź: 9·9·3=243
II sposób
Zgodnie z warunkami zadania interesują nas liczby, w których zapisie dziesiętnym jedna cyfra występuje dokładnie dwa razy, inna — dokładnie raz. Niech a oznacza niezerową cyfrę. Może ona wystąpić dwukrotnie w zapisie liczby trzycyfrowej na 3 sposoby
liczba kombinacji
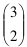

Puste pozycje dziesiątek i jedności możemy wypełnić na 9 sposobów, bo tyle jest cyfr różnych od a. Z kolei pozycję setek możemy wypełnić tylko na 8 sposobów, gdyż nie możemy tam wpisać cyfry 0. Ponieważ mamy 9 możliwych wartości a, łącznie mamy 2·9·9+9·8, czyli 234 liczby o powtarzającej się cyfrze różnej od 0 (reguła mnożenia, następnie reguła dodawania).
Para 0-0 może wystąpić tylko w jeden sposób, jako że 0 nie może wystąpić na pozycji setek, na której może jej towarzyszyć dowolna cyfra niezerowa; mamy zatem 9 możliwości. Łącznie mamy więc 234 + 9, czyli 243 liczby spełniające warunki zadania.